Quantum Entanglement

1. Mathematical description

We will not consider the EPR paradox, so we will consider quantum entanglement for only one property. Consider a quantum system having two particles. Each particle can be in two states: 0 and 1. In general, the wave function has the following form
\begin{equation} |\psi\rangle = c_{00}|00\rangle + c_{01}|01\rangle + c_{10}|10\rangle + c_{11}|11\rangle . \end{equation} If the particles are independent, then the wave function has the form

\begin{eqnarray} |\psi\rangle = (c_0^1|0\rangle + c_1^1|1\rangle)(c_0^2|0\rangle + c_1^2|1\rangle) = \nonumber
c_{00}|00\rangle + c_{01}|01\rangle + c_{10}|10\rangle + c_{11}|11\rangle . \end{eqnarray}

If the system is in an entangled state, then its wave function will be as follows

\begin{equation} |\psi\rangle = c_{00}|00\rangle + c_{11}|11\rangle \end{equation}
or
\begin{equation} |\psi\rangle = c_{01}|01\rangle + c_{10}|10\rangle . \end{equation}

2. Semantic Net Description

Let a point particle be in two basic states ZERO and ONE.

class State(Enum):
        ZERO = 1
        ONE = 2

class Leaf0(Component): # <<Atom>>
    """ Concept = Particle in the base state 0 """
    def __init__(self):
        self.state = State.ZERO
class Leaf1(Component): # <<Atom>>
    """ Concept = Particle in the base state 1 """
    def __init__(self):
        self.state = State.ONE

Then a quantum particle can be defined as follows

class MixOne(Leaf0, Leaf1):
    """ Concept = Quantum particle """
    w0 = (1.0/math.sqrt(2.0))*complex(math.cos(0.0), math.sin(0.0))
    w1 = (1.0/math.sqrt(2.0))*complex(math.cos(0.0), math.sin(0.0))
    
    def __init__(self):
        random.seed()
        p = self.w0.conjugate()*self.w0
        p = abs(self.w0.real)**2
        r = random.random()
        print (p,r)
        if r <= p.real:
            self.struc = Leaf0() 
        else:
            self.struc = Leaf1() 

Here we have a name conflict (‘state’ attribute and ‘Run’ operation). We use multiple inheritance emulation. Let’s introduce the ‘struc’ attribute to store the object-structure. The difference between emulation and true inheritance is that the ‘state’ attribute is not inherited by the ‘MixOne’ class, but is encapsulated in a object-structure.

The complete code is here https://github.com/vgurianov/qm/software/entaglement.py.

Let us now consider how a composite quantum object can be created. Wave function as a frame net is depicted in the picture Fig.5

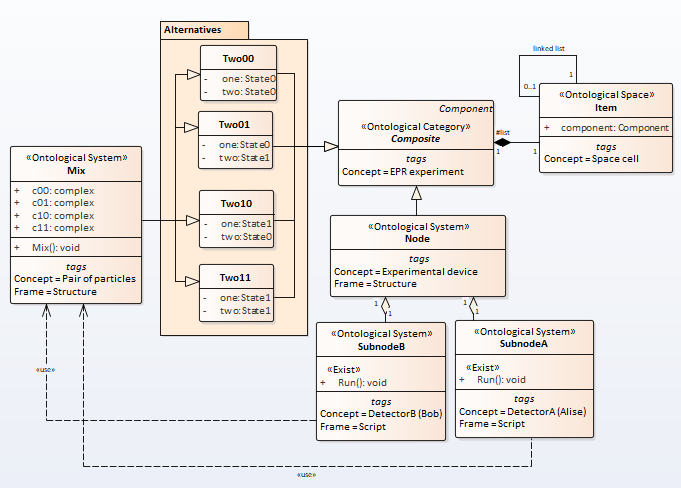Fig.5. The entanglement wave function

Note: This diagram is in a simplified form.
In general systems theory, this method is called the enlargement method or the coarsening method.
This simplification allows you to focus on essential relationships and hides unimportant details.

Let us compose the base states as possible alternatives. To create basic states, let’s place the particles in the extreme cells of space. For example, the base state \(|01\rangle\) would be defined by the following code

class Two01(Composite):
    def __init__(self): # <<System>>
        super().__init__(3) # run __init__ from Composite
        self.head.component = Leaf0()
        self.tail.component = Leaf1()

It should be noted that in this case, the basic states ‘Leaf0’ and ‘Leaf1’ are used, and not ‘MixOne’.
Let’s emulate multiple inheritance, for this we will introduce the fields ‘head’ and ‘tail’

class Mix(Two00,Two01,Two10,Two11):  # <<System>>
    # entaglement:
    w00 = 0.0*complex(math.cos(0.0), math.sin(0.0))
    w01 = (1.0/math.sqrt(2.0))*complex(math.cos(0.0), math.sin(0.0))
    w10 = (1.0/math.sqrt(2.0))*complex(math.cos(0.0), math.sin(0.0))
    w11 = 0.0*complex(math.cos(0.0), math.sin(0.0))

    def __init__(self):
        
        random.seed()
        p00 = abs(self.w00)**2
        p01 = abs(self.w01)**2
        p10 = abs(self.w10)**2
        p11 = abs(self.w11)**2
        r = random.random()
        if r <= p00:
            t = Two00()
        elif r > p00 and r <= p01+p00:
            t = Two01()
        elif r > p01+p00 and r <= p10+p01+p00:
            t = Two10()
        else:
            t = Two11()
        self.head = t.head.component
        self.tail = t.tail.component

The difference between emulation and true inheritance is that the ‘head’ and ‘tail’ attributes are not inherited by the ‘Mix’ class, but is encapsulated in a object-structure.
We introduce the global variable PP to model quantum nonlocality.
Particle state measurement activities are encapsulated in classes A and B

class A(Composite): # <<System>> 
    """ Concept =  Alice """
    def __init__(self):
        super().__init__(1) # run __init__ from Composite

    def Run(self):
        global PP
        PP = Mix() # the wave function collapse
        self.m1 = PP.head.state  # measurement
        return self.m1

    def accept(self, _m): # accept measurement
        self.m2 = _m  


class B(Composite): # <<System>>  
    """ Concept =  Bob """
    def __init__(self):
        super().__init__(1) # run __init__ from Composite
        
    def Run(self):
        # Bob
        global PP
        self.m2 = PP.tail.state # measurement
        return self.m2

    def accept(self, _m): # accept measurement
        self.m1 = _m  

An experiment with quantum entanglement is modeled by the ‘Node’ class.

            # Alise 
            m1 = self.head.component.Run()
            # Bob
            m2 = self.tail.component.Run()
            
            # message from Alice to Bob and from Bob to Alice
            self.head.right.component = m1
            self.tail.component.accept(self.head.right.component)
            self.head.right.component = m2
            self.tail.component.accept(self.head.right.component)
            
            # collection and processing of data    
            if m1 != m2:
                confirm = confirm + 1
            else:
                nonconfirm = nonconfirm + 1

The first block of code models the measurements that Alice and Bob take. The second block models the exchange of messages between Alice and Bob. The third block models the data collection and processing subsystem, which we show as an activity to simplify the code.

The message exchange order will be as follows,Fig.6.

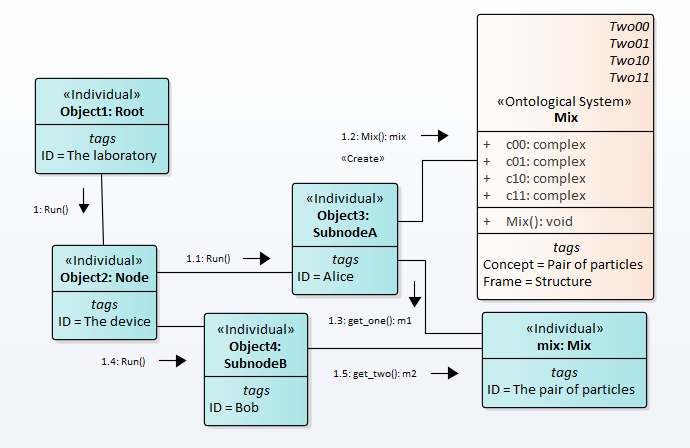
Fig.6. Sequence of messages

As soon as Alice takes a measurement for the first particle, Bob can immediately find the state of the second particle, regardless of the distance between particles. This is possible because an instance of the ‘Mix’ class already exists.

The complete code is here https://github.com/vgurianov/qm/software/entaglement.py.
The result of the script execution

==================== RESTART:  
count =  5000 confirm= 5000 nonconfirm= 0
confirm =  1.0
nonconfirm =  0.0

In conclusion, let’s touch on one more topic. The UML2 SP language makes it possible to describe two more effects similar to quantum entanglement but of a completely different nature.

1. Copy pointers. If we place copies of the object pointer in the extreme cells of the space, then we get the measurement correlation (or anti-correlation, if we define the ‘get()’ method)

   head = MixOne()
   tail = head
   print(head.struc.state, tail.struc.state)
   

2. Class variables. If you use class variables then for all instances these variables will have the same value. Let’s define in the ‘MixOne’ class a variable of the ‘attr’ class and assign a value to it

   head = MixOne()
   tail = MixOne()
   print(head.attr, tail.attr)
   

   The result of the script execution

   ==================== RESTART:  
   State.ONE State.ONE
   State.ZERO State.ZERO
   

The fact that the UML2 SP language allows one to describe such effects does not, of course, mean that they exist in nature.

Class attributes can be used to model nonlocality.

class Cell(object):
    def __init__(self):
        pass
        
    def __init__(self):
        self.content = None
        self.right = None
        self.left = None

space = Cell()
space.right = Cell()
space.right.right = Cell()


class Composite(): # <<Category>>
    """ Concept = Composite system """

    head = space
    tail = space.right.right
    def __init__(self, list_l):
        pass
    

class Two01(Composite): # <<System>>

    def __init__(self):
        #super().__init__(3) # run __init__ from Composite
        self.head.content = 0
        self.tail.content = 1

class A(Composite): # <<System>> 
    """ Concept =  Alice """
    def __init__(self):
        pass
class B(Composite): # <<System>> 
    """ Concept =  Bob """
    def __init__(self):
        pass

# ------------
qs = Two01()
cs = A()
print(qs.head.content, cs.head.content)
cs = B()
print(qs.tail.content, cs.tail.content)

The result is

====================== RESTART: 
0 0
1 1

In our opinion, this hypothesis seems more plausible than the hypothesis with a global variable.