Uncertainty principle

1. Matematical discription

Let \(\hat {L}\) and \(\hat {M}\) be self-adjoint operators and their commutator \([{\hat {L}},{\hat {M}}]={\hat {L}}{\hat {M}}-{\hat {M}}{\hat {L}}\) be non-zero. Denote by \(\mid l_i\rangle\) and \(\mid m_j\rangle\), \(i,j=1,2\) the eigenfunctions of these operators.

Let wave function \(\mid a\rangle\) be determined in \(l\)-basis

\begin{equation} |a\rangle = a_1|l_1\rangle + a_2|l_2\rangle = \langle l_1|a\rangle |l_1\rangle + \langle l_2|a\rangle |l_2\rangle \end{equation}
Both \(m\)- and \(l\)-basis can be transform into each other.

\begin{eqnarray} \mid l_1\rangle = \langle m_1 \mid l_1\rangle \mid m_1\rangle + \langle m_2 \mid l_1\rangle \mid m_2\rangle \nonumber
\mid l_2\rangle = \langle m_1\mid l_2\rangle \mid m_1\rangle + \langle m_2\mid l_2\rangle \mid m_2\rangle \end{eqnarray}

Now we can to transform \(\mid a \rangle\) wave function to \(m\)-basis.

\begin{multline} |a\rangle = a_1 |l_1\rangle + a_2 |l_2\rangle = \nonumber
= a_1 (\langle m_1 \mid l_1\rangle \mid m_1\rangle + \langle m_2 \mid l_1\rangle \mid m_2\rangle ) + a_2 ( \langle m_1\mid l_2\rangle \mid m_1\rangle + \langle m_2\mid l_2\rangle \mid m_2\rangle ) = \nonumber
= (a_1 \langle m_1 \mid l_1\rangle + a_2 \langle m_1\mid l_2\rangle)\mid m_1\rangle + (a_1 \langle m_2 \mid l_1\rangle + a_2 \langle m_2\mid l_2\rangle)\mid m_2\rangle = \nonumber
= b_1 \mid m_1\rangle + b_2 \mid m_2\rangle , \end{multline}

where

\begin{eqnarray} b_1 = a_1 \langle m_1 \mid l_1\rangle + a_2 \langle m_1\mid l_2\rangle \nonumber \
b_2 = a_1 \langle m_2 \mid l_1\rangle + a_2 \langle m_2\mid l_2\rangle \end{eqnarray}

i.e. \(b = Ua\), where \(U\) is a unitary operator and \(a^+=(a_1,a_2)\), \(b^+=(b_1,b_2)\). A unitary operator satisfies \(U^*U = UU^* = I\), where \(U^*\) is the adjoint of \(U\), and \(I\) is the identity operator. Suppose that the unitary operator has form

\(U = \begin{pmatrix} 1/\sqrt{2} & 1/{\sqrt{2}} \\ -1/\sqrt{2} & 1/\sqrt{2} \end{pmatrix}\)
then we get uncertainty principle. Let be \(a_1 = 1, a_2 = 0\). From (7) we get \(b_1 = 1/\sqrt{2}\) and \(b_2=1/\sqrt{2}\). Let be \(a_1 = 1/\sqrt{2}, a_2 = 1/\sqrt{2}\) then we get \(b_1 = 1\) and \(b_2=0\).

As we can see, if the measurement of one quantity is accurate, then the other quantity is completely uncertain.

2. Semantic Net Description

Wave function as a semantic net is depicted in the picture

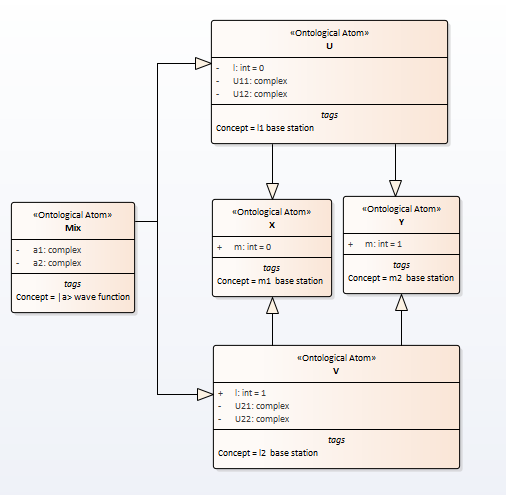Fig.4. The uncertainty principle wave function

The name conflict (l and m) is resolved twice. First in the constructor of classes U and V, then in the constructor of the MIX class.

3. Software and results

Experiment result is depicted in table

№	\(\mid m_1\rangle\)	\(\mid m_2\rangle\)	\(\mid l_1\rangle\)	\(\mid l_2\rangle\)
1	1.0	0.0	0.497	0.503
2	0.499	0.501	1.0	0.0

The complete code is here https://github.com/vgurianov/qm/software/uncertainty.py.